源于麦克斯韦方程组的优化算法

针对电磁学中优化问题的目标函数复杂、局部最优点多、维度极高等难点，从电磁学的基本理论出发，研究了一种更适用于求解电磁学优化问题的优化算法。该算法关注到同轴线的接地回路随信号源频率的变化而发生改变这一现象，将优化问题中自变量和目标函数的关系转化成该电路中两个导体之间的位置关系。通过麦克斯韦方程组中的法拉第电磁感应定律和电荷守恒定律对电流进行分析，用左手定律将电流转化为安培力，驱动电路中的导体运动，并通过参数的设置使其最终达到另一个导体所代表的目标函数最小值的位置。由于麦克斯韦方程组是推导该算法迭代公式的核心物理定律，我们将该优化算法命名为“源于麦克斯韦方程组的优化算法（MEDO）”。

通过使用标准的适应度函数对MEDO算法进行有效性和稳定性测试，可以证明该算法具有较高的准确性和稳定性。在此基础之上，MEDO算法被成功用来解决了多种电磁学相关工程问题，包括：线性天线阵列综合、频率选择表面结构参数设计和典型波形的参数提取等。这些问题在电磁学中有非常重大的意义，但是由于它们维度高、非线性强、对稳定性要求高，所以对优化算法来说是一个很大的挑战。从优化结果来看，MEDO在解决这类型的问题上可以取得比遗传算法、粒子群算法等这些主流的优化算法更为优异的结果。综上所述，从电磁学中推导出的MEDO优化算法在解决电磁学中优化问题时具有非常大的潜力。

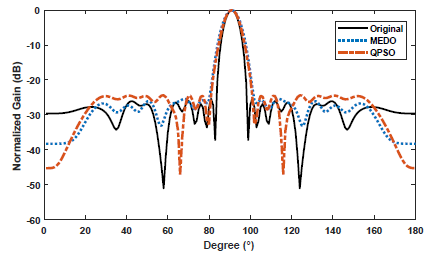
图 1 MEDO用于阵列损毁修复及与QPSO优化算法的效果对比

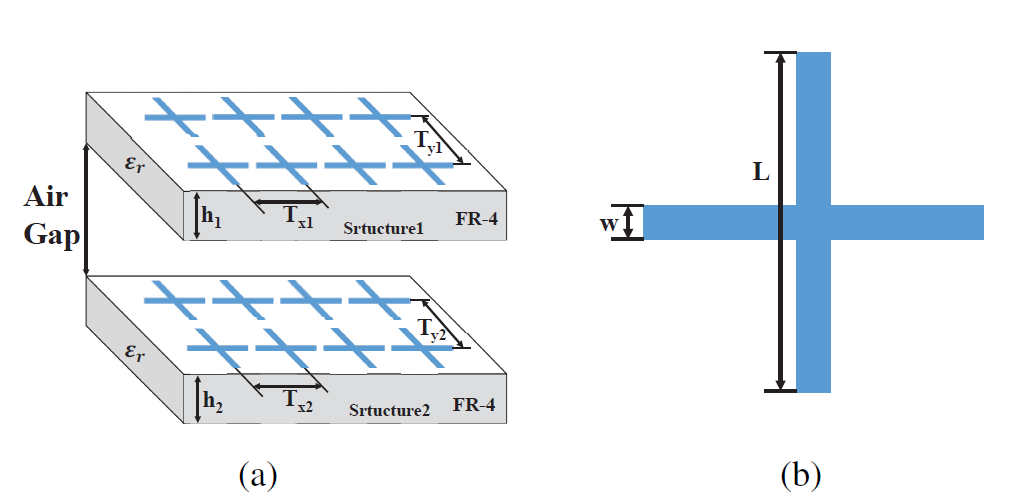
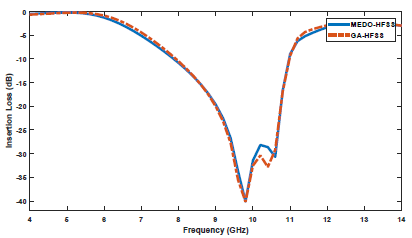
图 2 MEDO用于双层FSS设计及与GA优化算法的设计结果对比

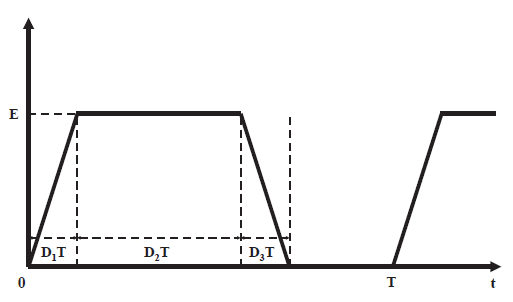
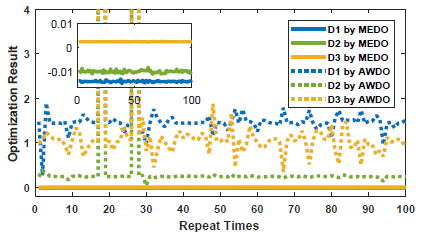
图 3 MEDO用于梯形波时域参数提取及其与AMEDO算法的提取稳定度对比

1.      Su Donglin, Li Lilin, et al. A new optimization algorithm applied in electromagnetics - Maxwell's equations derived optimization[J]. SCIENCE CHINA-INFORMATION SCIENCES, 2020,63(10)