针对有限大型多尺度周期/准周期阵列结构难于进行高效精准的电磁分析问题,我们在只面向周期结构的内存高效DGTD方法基础上进行了三个方面的优化。首先是通过矩阵复用技术,实现了准周期结构的高效仿真。在仿真过程中,只需保存每种阵元类型中的一个阵元,使内存消耗与阵元类型数目为正比,而不是与阵元总数成正比,在很大的程度上降低了内存消耗。同时在准周期结构中允许各种类型的单元任意混合存在,如图1所示。然后针对结构的多尺度特性,提出了嵌套模型,该模型通过将周期/准周期结构中单元的电大尺寸部分和电小尺寸部分进行分离,使一个单元成为两个亚单元,如图2所示,分别进行分析和计算,能够降低结构复杂度,提高计算效率。最后,为了突破CFL条件的限制,将隐式龙格-库塔时间步进方法引入已经改进的周期/准周期内存高效DGTD方法,增大了时间步长,从而节省仿真时间。仿真大型有限周期结构的传统方法都是先将结构当作无限大周期结构来处理,然后通过Floquet定理选取一个标准阵元代替其余所有单元进行仿真,但是该方法忽略了边缘效应,仿真的精度较低。周期/准周期结构的内存高效DGTD方法在节省内存的同时还考虑阵元的边缘效应,精度很高,可广泛应用于MIMO天线、相控阵天线、智能天线、超构材料与超构表面等的电磁分析。
针对子区域层级DGTD方法在时间步进的过程需要求解大量线性方程且非常耗时的问题,我们采用MPI消息传递模型实现了DGTD并行算法,该算法带有自动负载均衡策略,能够有效地提高多尺度电磁问题的求解效率。负载均衡策略具有一键式的特性,首先我们分别从四面体或者六面体元素剖分的算例中提取一个计算负荷(CPU时间)和自由度的关系曲线,如图3所示。然后基于贪心算法,求解算例多进程时最优的子区域分配方式,最后优化子区域的交接面以达到进程负载均衡的目的,其具体流程如图4所示。整个方案仅涉及DGTD方法预处理的部分,无需多次组装系统矩阵,可以有效加快大型多尺度电磁算例的仿真速度。该并行子区域层级DGTD方法被用于微带线的集总端口电压求解、低通滤波器的散射参数分析、导弹雷达散射截面计算和机箱电磁屏蔽效能分析等数值算例。其结果与采用传统的FDTD方法得到的结果一致,证明了该方法的准确性。通过上述算例在多进程下的加速比分析,验证了负载均衡策略的有效性和并行算法的高效性。采用所提出的并行DGTD方法可以有效地减少总执行时间,这对于解决大规模、多尺度的电磁问题具有重要意义。
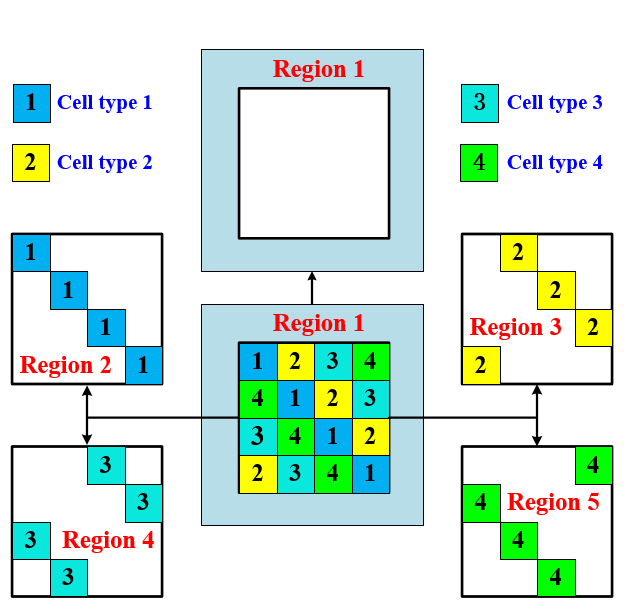
图1 准周期结构
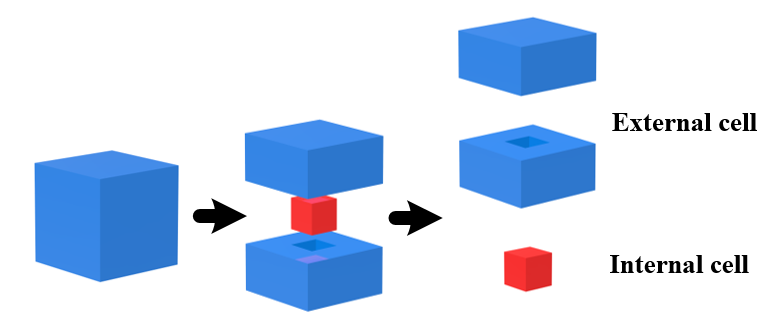
图2 嵌套周期单元模型
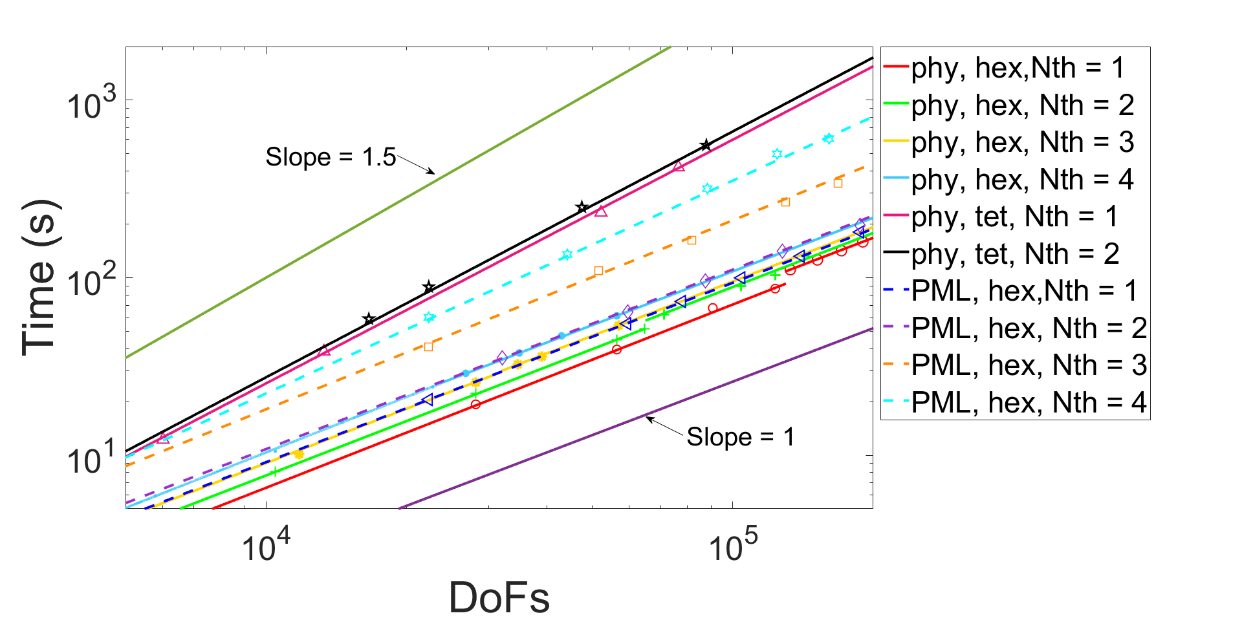
图3 物理和PML区域中,不同元素类型和阶数的DoFs与3000步时间开销的关系。(phy表示物理区域,hex表示六面体元素,tet表示四面体元素,Nth表示元素阶数。)
论文:
Pengfei Wen, Qiang Ren, Jiefu Chen, et al. Improved memory efficient subdomain level discontinuous Galerkin time domain method for periodic/quasi-periodic structures[J]. IEEE Transactions on Antennas and Propagation, vol. 68, no. 11, pp. 7471-7479, Nov. 2020, DOI:10.1109/TAP.2020.2998215.
J. Mi, Q. Ren and D. Su. Parallel Subdomain Level DGTD Method with Automatic Load Balancing Scheme with Tetrahedral and Hexahedral Elements[J]. IEEE Transactions on Antennas and Propagation, DOI: 10.1109/TAP.2020.3026489.